Tricks to solve Average Problems in exams

Average

What is Average?
The result obtained by adding several quantities together and then dividing this total by the number of quantities is called Average.
The main term of average is equal distribution of a value among all which may distribute persons or things. We obtain the average of a number using formula that is sum of observations divided by Number of observations.
Here is average based some fact and formula and some average shortcut tricks examples. The problem is given in Quantitative Aptitude which is a very essential paper in ssc exam. Given below are some more example for practicing.
Formula:

• Average: = (Sum of observations / Number of observations).

Find the Average Speed

• If a person travels a distance at a speed of x km/hr and the same distance at a speed of y km/hr then the average speed during the whole journey is given by-   
• If a person covers A km at x km/hr and B km at y km/hr and C km at z km/hr, then the average speed in covering the whole distance is- When a person leaves the group and another person joins the group in place of that person then-

• If the average age is increased,
  Age of new person = Age of separated person + (Increase in average × total number of persons)
• If the average age is decreased,
  Age of new person = Age of separated person - (Decrease in average × total number of persons)

When a person joins the group-In case of increase in average

• Age of new member = Previous average + (Increase in average × Number of members including new member)

In case of decrease in average

• Age of new member = Previous average - (Decrease in average × Number of members including new member)

In the Arithmetic Progression there are two cases when the number of terms is odd and second one is when number of terms is even.

• So when the number of terms is odd the average will be the middle term.
• when the number of terms is even then the average will be the average of two middle terms.

Some Important Examples
 Examples 1: what will be the average of 13, 14, 15, 16, 17?
Solution: Average is the middle term when the number of terms is odd, but before that let’s checks whether it is in A.P or not, since the common difference is same so the series is in A.P. So the middle term is 15 which is our average of the series.
Example 2: What will be the average of 13, 14, 15, 16, 17, 18?
Solution: We have discussed that when the number of terms are even then the average will be the average of two middle terms.
Now the two middle terms are 15 and 16, but before that the average we must check that the series should be A.P. Since the common difference is same for each of the term we can say that the series is in A.P. and the average is (16+15)/2 = 15.5
Example 3:The average of five numbers is 29. If one number is excluded the average becomes 27. What is the excluded number ?
Answer :
let the excluded number is
= (29 x 5) – ( 27 x 4 )
= 145 – 108
= 37 .
Example 4: Find the average of first 20 natural numbers?
Answer:
Sum of first n natural numbers = n ( n + 1 ) /2
So, we can find easily average of first 20 natural numbers 20 x 21 / 2 = 210
So, then Required average is = 210 / 20 = 10.5.
Example 5
Find the average of first 20 multiplies of 5 .
Answer:
Required average = 5 ( 1 + 2 + 3 +……………….. + 20) /20
= ( 5 x 20 x 21 / 20 x 2) = 2100 / 40 = 52.5 .
So the Required average is 52.5.
Question 1. The average of 8 numbers is 20. The average of first two numbers is 15.5 and the average of next three number is  If the 6^th number is 4 and 7 less by the 7^th and the 8^th numbers respectively then what will be the 8^th number?
(1)     25
(2)     22
(3)     35
(4)     30
Solution:
Short Trick: 
Sum of all = 160
Sum of first 5 = 95 coming from

sum of last 3 = 65
x + x + 4 + x + 7 = 65
 18 + 22 + 25
Answer: 1
Question 2: The average temperature from Monday to Wednesday is 37⁰C while the average temperature from Tuesday to Thursday is 34⁰C. The temperature of Thursday is  times to that of Monday. Find the temperature of Thursday?
(1)     36⁰C
(2)     33⁰C
(3)     37⁰C
(4)     34⁰C
Solution:



Short Trick: 
Mon + Tues + Wed = 111
Tues + Wed + Thurs + 102 (diff. = 9)
Thursday = Thursday = 
Question 3:  Of the three numbers whose average is 60, the first is one-fourth of the sum of the others.  The first number is
(1)     30
(2)     36
(3)     42
(4)     45
Solution:

x + y + z = 180 …………(i)
 then 4x + y + z
Putting the  value of y + z in
Equation …………….(i) x + 4x = 180
5x = 180 x = 36
Sum = 
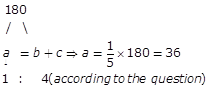
Question 4:  The average of marks obtained by 120 candidates in a certain examination is 35. If the average marks of passed candidates is 39 and that of the failed candidates is 15, what is the number of candidates who passed the examination?
(1)     100
(2)     120
(3)     140
(4)     160
Solution:
Let the number of passed candidates be x
Then total marks = 120 x 35 = 39x + (120 – x) x 15
Or,  4200 = 39x + 1800 – 15x
Or, 24x = 2400
x = 100
Number of passed candidates = 100
Short Trick:
Pass       Fail
39          15
\         /
35
/     \
20     4
      5  :  1
Hence, total number of passed candidates

Question 5: The average weight of 8 persons is increased by 2.5 kg when one of them who weight 56 kg is replaced by a new man. The weight of the new man is
(1)     73 kg
(2)     72 kg
(3)     75 kg
(4)     80 kg
Solution: 
Aw₂ – AW₁ = 2.5


Total weight₁ – Total weight₂  = 20.0 kgs
This difference is because of the new man.
Hence the weight of the new man = 56 + 20  = 76 kgs.
Short Trick: 
56 + 8 x 2.5
= 76 kgs